Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Кинетика катализируемых ферментами реакций
Кинетика простых ферментативных реакций с одним и двумя субстратами
Уравнение Михаэлиса - Ментен

Предположим теперь, что в нашем распоряжении имеется целый ряд экспериментальных данных по определению скорости ферментативной реакции (рис. 3.7) и перед нами стоит задача выразить эти данные в математической форме. Информация типа показанной на рис. 3.7 часто позволяет сделать следующие выводы качественного характера:

1. При относительно низких концентрациях субстрата реакция имеет первый порядок по субстрату. (Напомним, что если v = k∙sⁿ, где k — константа, то n называют порядком реакции.)

2. По мере повышения концентрации субстрата порядок реакции по субстрату постепенно снижается от единицы до нуля.

3. Скорость реакции пропорциональна общему количеству фермента в реакционной смеси.

На базе экспериментальных данных такого рода в 1902 г. Анри предложил следующее выражение для скорости ферментативной реакции:

(3.3)

В уравнении (3.3) учтены все три указанные выше закономерности. Обратите внимание, что при s, равном K_m, v = v_max/2. Во избежание недоразумений, связанных с употреблением в литературе различных символов и сокращений, подчеркнем, что s обозначает концентрацию свободного субстрата в реакционной смеси, а е₀ — общую концентрацию фермента как в свободном, так и в связанном виде (см. ниже).

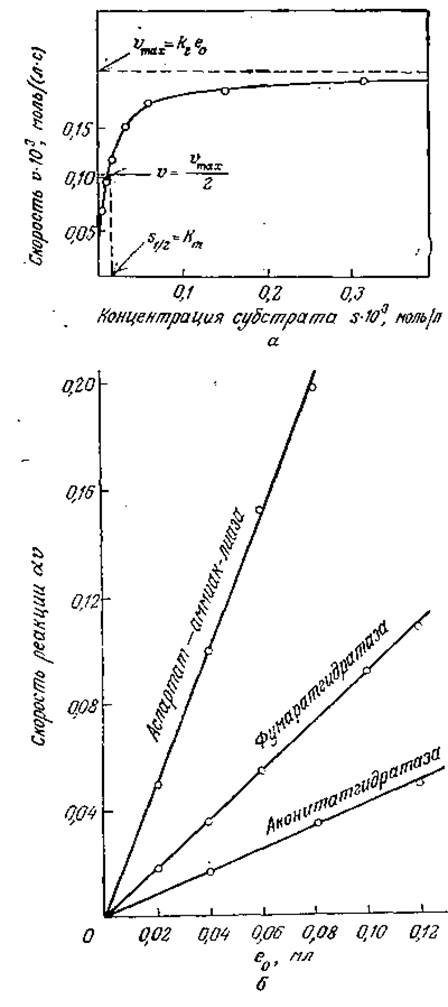
РИС. 3.7. Экспериментальное изучение кинетики катализируемых ферментами реакций.

а — зависимость скорости реакции от концентрации субстрата при постоянной концентрации фермента. [Воспроизведено из работы: Laidler К. I., The Chemical Kinetics of Enzyme Action, p. 64, The Clarendon Press, Oxford, 1958, по данным, опубликованным ранее в статье: Quellet L., Laidler К. J., Morales M. F., Molecular Kinetics of Muscle Adenosine Triphosphate, Arch. Biochem. Biophys., 39, 37 (1942).] б — зависимость скорости реакции (изменение оптической плотности при 200 нм за 1 мин) от концентрации фермента при постоянной концентрации субстрата. Из работы: Диксон М., Уэбб Э., Ферменты, т. 1—3. — М.: Мир, 1982.)

Хотя Анри дал теоретическое толкование уравнению (3.3) на базе гипотетического механизма реакции, его доказательство, равно как и близкое обоснование, предложенное в 1913 г. Михаэлисом и Ментен, в настоящее время считается в общем случае не строгим. В то же время в этой главе мы неоднократно и не без успеха будем применять общий ход рассуждений Михаэлиса и Ментен (так и не нашедший до сих пор строгого подтверждения) для разработки более сложных моделей кинетики ферментативного катализа. Поэтому сначала мы рассмотрим основные положения гипотезы Михаэлиса — Ментен.

В качестве одного из исходных положений принимают, что фермент Е и субстрат S, вступая в реакцию, образуют комплекс ES, который затем диссоциирует на продукт реакции Р и свободный (несвязанный) фермент Е:

В этом механизме учтены как рассмотренное выше образование фермент-субстратного комплекса, так и регенерация катализатора в исходной форме по завершении последовательности реакций. Уравнения (3.4) в принципе верны, хотя и чрезмерно упрощены.

Анри, а также Михаэлис и Ментен предположили, что реакция (3.4а) обратима, и, следовательно, в соответствии с законом действующих масс мы можем записать:

Здесь s, е и (es) обозначают концентрации S, E и ES соответственно. Кроме того, принимается, что процесс разложения комплекса на продукт реакции и свободный фермент необратим:

Поскольку весь фермент находится или в свободной, или в связанной форме, то

где е₀ — общая концентрация фермента в системе, известная из исходных данных и равная количеству фермента, загруженного в реактор. Теперь путем исключения (es) и е из трех последних уравнений можно получить уравнение (3.3), в котором v_max = k₂e₀. Обычно, говорят, что реакция характеризуется уравнением Михаэлиса — Ментен, если ее скорость может быть описана уравнением (3.3), хотя в разработку и подтверждение правильности этого выражения внесли не меньший вклад и другие исследователи. Параметр v_mах называют максимальной или предельной скоростью, a K_mизвестна как константа Михаэлиса. Уравнение Михаэлиса — Ментен удачно описывает кинетику многих катализируемых ферментами реакций, но тем не менее оно не универсально. В последующих разделах и в упражнениях мы рассмотрим ряд модифицированных вариантов

этого уравнения, которые точнее описывают конкретные ферментативные реакции, протекающие в специфических условиях.

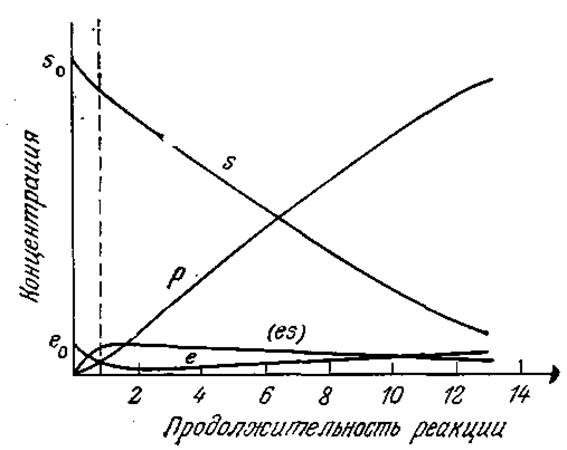
РИС. 3.8. Изменение концентраций веществ в реакции

Бриггс и Холдейн пришли к уравнению (3.3) другим путем, который, как было показано позднее путем экспериментального изучения кинетики и математического анализа, носит наиболее общий характер. Если реакция осуществляется в закрытом сосуде при энергичном перемешивании, то уравнения материального баланса для субстрата и фермент-субстратного комплекса можно записать следующим образом:

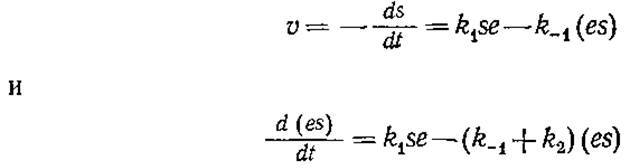
С учетом выражения (3.7) эти два уравнения представляют собой систему двух обычных дифференциальных уравнений с двумя неизвестными, s и (es). Понятно, что соответствующие начальные условия при t = 0 выражаются следующим образом:

s(0) = s₀ (es) (0) = 0

Эти уравнения нельзя решить аналитически, но путем интегрирования с помощью компьютеров можно найти зависимости концентраций S, Е, ES и Р от времени. Полученные таким путем результаты приведены на рис. 3.8; очевидно, что после короткого стартового периода можно с весьма большой точностью принять, что

Ключевым пунктом анализа Бриггса и Холдейна явилось допущение о правильности условия (3.8). Можно показать, что для нашего случая катализируемой ферментом реакции в закрытой системе это допущение, называемое обычно приближением квазиравновесного состояния, справедливо при условии достаточно малой величины отношения e₀/s₀. Если же начальная концентрация субстрата сравнима с общей концентрацией фермента, то допущение (3.8) может оказаться неверным. В большинстве случаев, однако, количество ферментного катализатора намного меньше количества реагентов; в такой ситуации после стартового периода реакции выражение (3.8) можно считать применимым с достаточно высокой точностью.

Если далее, следуя рассуждениям Бриггса и Холдейна, из приведенных выше уравнений с помощью выражения (3.7) исключить е и (es), то мы придем к уравнению

Таким образом мы получили выражение типа уравнения Михаэлиса — Ментен, в котором

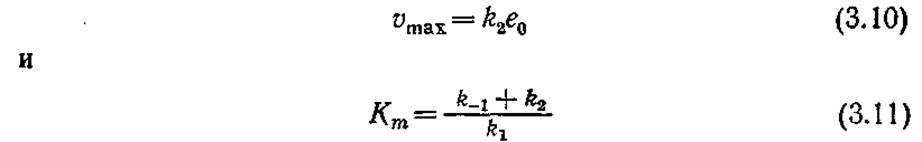
Обратите внимание на то, что здесь K_m по физическому смыслу уже не является константой диссоциации.

Располагая математическим выражением для скорости реакции типа уравнения Михаэлиса — Ментен, мы можем определить изменения концентраций реагентов во времени путем интегрирования

Таким путем получаем, что

Разумеется, на практике это уравнение проще использовать для расчета времени t, необходимого для достижения определенных концентраций субстрата, а не наоборот.

Полезно сравнить ход реакции, предсказываемый уравнением (3.13), с результатами, полученными без приближения квазиравновесного состояния. Как показано на рис. 3.9, отклонения могут быть значительными, если общая концентрация фермента приближается к s₀, поэтому в таких случаях не следует применять уравнение Михаэлиса — Ментен. На рис. 3.10 приведен другой пример, а именно зависимость эстеразной активности от концентрации фермента. Здесь предсказываемая моделью Михаэлиса — Ментен линейная зависимость справедлива при малых концентрациях фермента, но также не соблюдается при более высоких концентрациях. Запомните, что для линейного участка кривой тангенс угла наклона равен k₂s/(K_m + s).

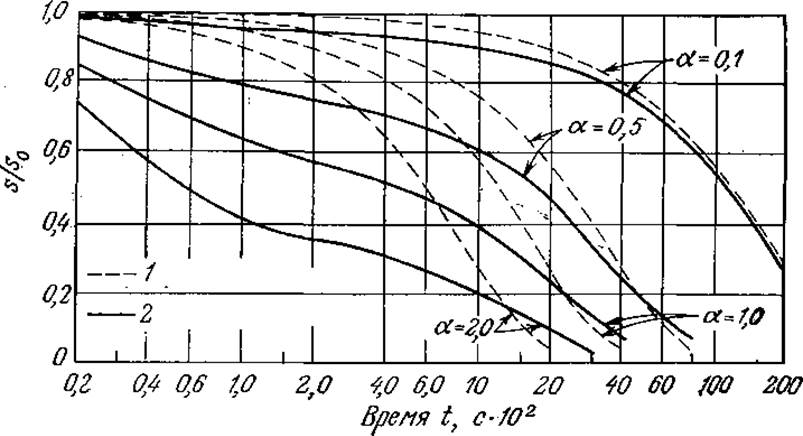
РИС. 3.9. Вычисленные зависимости степени гидролиза эфира ацетил-L-фенилаланина химотрипсином от продолжительности реакции в реакторе периодического действия. При больших величинах e₀/s₀ = a наблюдается значительное несоответствие между точным решением и решением в квазиравновесном приближении. [Воспроизведено с разрешения из статьи: Lim Н. С., On Kinetic Behavior at High Enzyme Concentrations, Amer. Inst. Chem. Eng. J., 19, 659 (1973).] 1 — решение в квазиравновесном приближении; 2 — точное решение.

В некоторых случаях в зависимости от скоростей отдельных стадий реакции приближение квазиравновесного состояния может оказаться справедливым и при больших значениях e₀/s₀. В частности, такая ситуация могла бы возникнуть, если бы комплекс ES диссоциировал гораздо быстрее, чем образовывался, т. е. если бы К_m была значительно большего. Однако обычно константа Михаэлиса очень мала и составляет от 10^-2 до 10^-5, поэтому такие случаи не типичны.

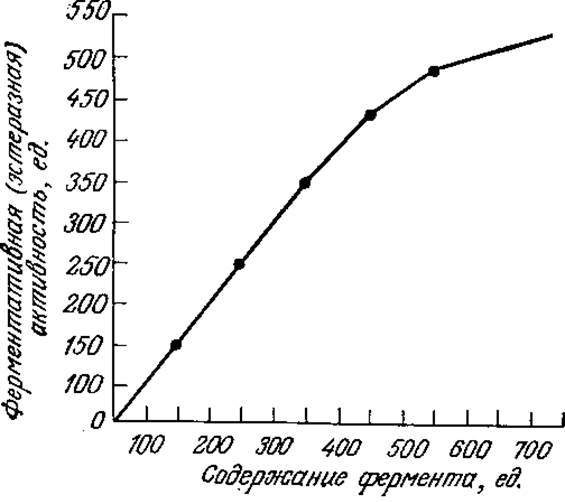
РИС. 3.10. При высоких начальных концентрациях фермента зависимость эстеразной активности от концентрации эстеразы не подчиняется уравнению Михаэлиса — Ментен. (Воспроизведено с разрешения из работы: Frobisher М., Fundamentals of Microbiology, 8th ed., p. 61, W. B. Saunders Co., Philadelphia, 1968.)

Отсюда следует, что если концентрация фермента сравнима с s₀, то, как правило, у нас нет достаточных оснований для упрощения модели кинетики соответствующего процесса с использованием приближения квазистационарного состояния. Относительная концентрация фермента может достигать больших значений, например, если работа ферментативного реактора продолжается и_: тогда, когда большая часть субстрата уже подверглась превращению. В таком случае s уменьшается до значений, сравнимых с e₀, и на последнем этапе процесса уравнение Михаэлиса — Ментен может уже не отражать его реальной кинетики. К счастью, в этот период реакция резко замедляется и поэтому, как правило, уже не представляет практического интереса. Концентрация субстрата вблизи фермента может быть незначительной и при проведении ферментативных реакций на поверхности раздела фаз; реакции такого типа мы рассмотрим в разд. 4.4. В таких случаях следует учитывать и скорость переноса субстрата к границе раздела фаз. Ограничения, свойственные модели Михаэлиса — Ментен, выявились лишь в самое последнее время, и поэтому соответствующее уравнение все еще широко используется при изучении и проектировании ферментативных реакторов. Хотя в некоторых ситуациях равновесное приближение и уравнение Михаэлиса — Ментен нельзя считать достаточно точными, в целом они оказались очень полезными инструментами исследования, и в этом качестве мы часто будем их применять и в дальнейшем изложении.

Говоря о простом уравнении Михаэлиса — Ментен, нельзя не упомянуть, что точно таким же математическим выражением широко пользуются для оценки скоростей многих реакций, ускоряемых твердыми катализаторами. Уравнение (3.3) в химической технологии называется уравнением Ленгмюра — Хиншелвуда или Хоугена — Уотсона. Поскольку в химической и нефтяной промышленности широко применяются реакции на синтетических твердых катализаторах, анализу и проектированию таких каталитических реакторов было посвящено огромное число работ. В большей части этих работ использовали уравнение Ленгмюра — Хиншелвуда; следовательно, их результаты с успехом могут быть перенесены и на катализируемые ферментами реакции, описываемые уравнением Михаэлиса — Ментен. В последующих главах мы еще не раз встретимся с аналогиями и сходством между классической химической и биохимической технологиями, но в то же время узнаем и многие особенности, характерные только для биологических процессов.